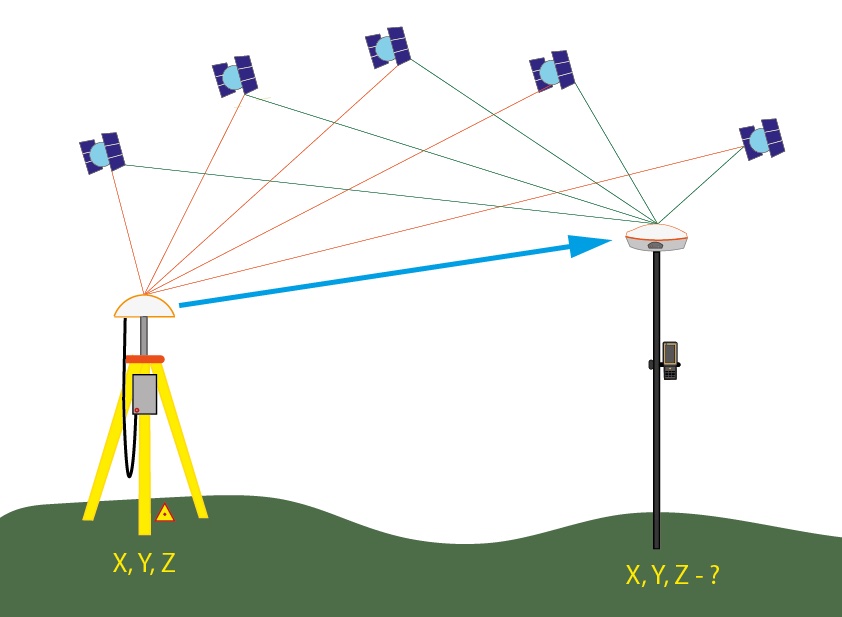
구조물 모니터링을 위한 RTK GPS의 아웃라이어 검출방법
RTK GPS는 mm 단위의 정밀도로 위치를 측정할 수 있어 구조물 모니터링, 지반 침하 측정, 댐 안전 관리 등에 널리 활용됩니다. 하지만 실제 현장에서 수집된 데이터에는 다양한 원인으로 인한 아웃라이어(이상치)가 포함되어 있어, 정확한 변위 분석을 위해서는 체계적인 데이터 정제가 필수적입니다.
이 글에서는 고정된 로버를 이용한 구조물 모니터링에 특화된 아웃라이어 검출 방법을 소개합니다.
RTK GPS 데이터의 특성과 아웃라이어 발생 원인
측정 데이터 구성
RTK GPS 로버에서 수집되는 주요 데이터는 다음과 같습니다:
- 위치 정보: 위도(Latitude), 경도(Longitude), 고도(Altitude)
- 시간 정보: 타임스탬프(Timestamp)
- 품질 지표:
- Fix 상태 (Fixed RTK, Float RTK, Single 등)
- 위성 개수 (Number of Satellites)
- HDOP/PDOP (정밀도 저하율)
- 정확도(Accuracy)
아웃라이어 발생 원인
구조물 모니터링에서 아웃라이어가 발생하는 주요 원인은 다음과 같습니다:
- 위성 신호 차단: 주변 건물, 나무, 지형에 의한 일시적 신호 손실
- 다중경로 오차(Multipath): 건물이나 구조물 표면에서 반사된 신호 수신
- Fix 상태 변화: Fixed RTK에서 Float 또는 Single로 저하
- 대기 조건: 전리층, 대류권 지연
- 장비 문제: 수신기 오작동, 안테나 위치 변화
고정 로버의 특수성
구조물 모니터링용 고정 로버는 일반적인 이동 측량과는 다른 특성을 가집니다:
- 이론적 정지 상태: 로버가 물리적으로 고정되어 있어 위치 변화가 없거나 매우 작음
- 미세 변위 감지: mm~cm 단위의 작은 변위를 감지해야 함
- 점진적 변화: 실제 구조물 변위는 급격하지 않고 서서히 발생
- 노이즈 vs 변위: 측정값의 대부분은 노이즈이며, 진짜 변위와 구분이 중요
따라서 급격한 점프는 대부분 아웃라이어로 간주할 수 있으며, 이를 제거하면서도 실제 구조물의 점진적 변화는 보존해야 합니다.
단계별 아웃라이어 검출 방법
1단계: 품질 기반 1차 필터링
가장 먼저 RTK GPS 자체의 품질 지표를 활용하여 명백히 낮은 품질의 데이터를 제거합니다.
Fix 상태 필터링
import pandas as pd
import numpy as np
def filter_by_fix_quality(df):
"""
RTK Fix 상태로 필터링
Fix Type: 4(Fixed RTK) 또는 5(Float RTK)만 유지
"""
# Fixed RTK만 사용 (가장 엄격)
df_filtered = df[df['fix_type'] == 4].copy()
# 또는 Float RTK까지 포함 (조금 더 관대)
# df_filtered = df[df['fix_type'].isin([4, 5])].copy()
return df_filtered
위성 품질 필터링
def filter_by_satellite_quality(df, min_satellites=12, max_hdop=1.5):
"""
위성 개수와 HDOP로 필터링
구조물 모니터링은 높은 품질 기준 적용
"""
df_filtered = df[
(df['num_satellites'] >= min_satellites) &
(df['hdop'] <= max_hdop)
].copy()
return df_filtered
권장 기준값 (구조물 모니터링):
- Fix Type: 4 (Fixed RTK)
- 위성 개수: 12개 이상
- HDOP: 1.5 이하
2단계: 기준 위치 설정 및 변위 계산
고정 로버의 경우, 절대 좌표보다는 기준점 대비 상대 변위를 분석하는 것이 효과적입니다.
def calculate_baseline_position(df):
"""
기준 위치 설정
중앙값을 사용하여 아웃라이어의 영향 최소화
"""
baseline = {
'latitude': df['latitude'].median(),
'longitude': df['longitude'].median(),
'altitude': df['altitude'].median()
}
return baseline
def calculate_displacement(df, baseline):
"""
기준점 대비 변위 계산 (미터 단위)
"""
from geopy.distance import geodesic
df = df.copy()
# 수평 변위 계산
displacements = []
for idx, row in df.iterrows():
point = (row['latitude'], row['longitude'])
base_point = (baseline['latitude'], baseline['longitude'])
horiz_disp = geodesic(base_point, point).meters
displacements.append(horiz_disp)
df['horizontal_displacement'] = displacements
# 수직 변위
df['vertical_displacement'] = df['altitude'] - baseline['altitude']
# 동-서, 남-북 성분 분리
earth_radius = 6371000 # 미터
df['east_displacement'] = (df['longitude'] - baseline['longitude']) * \
np.cos(np.radians(baseline['latitude'])) * \
np.pi * earth_radius / 180
df['north_displacement'] = (df['latitude'] - baseline['latitude']) * \
np.pi * earth_radius / 180
return df
3단계: 급격한 점프 제거
구조물은 급격히 변하지 않으므로, 연속된 측정값 사이의 큰 차이는 아웃라이어로 판단합니다.
def remove_sudden_jumps(df, jump_threshold=0.03):
"""
연속된 점 사이의 급격한 변화 제거
구조물 모니터링: 3cm 임계값 권장
"""
df = df.sort_values('timestamp').reset_index(drop=True)
df_clean = df.copy()
for col in ['horizontal_displacement', 'vertical_displacement']:
if col in df.columns:
# 연속된 값의 차이
diff = df[col].diff().abs()
# 급격한 점프 마스킹
jump_mask = diff > jump_threshold
jump_mask.iloc[0] = False # 첫 행 제외
df_clean = df_clean[~jump_mask]
df_clean = df_clean.reset_index(drop=True)
return df_clean
4단계: MAD 기반 아웃라이어 제거
MAD(Median Absolute Deviation)는 중앙값 기반 방법으로, 극단값에 매우 강건하여 고정 로버에 이상적입니다.
def remove_outliers_mad(df, mad_threshold=3.5):
"""
MAD 기반 아웃라이어 제거
중앙값 기반이므로 극단값에 강건
"""
df_clean = df.copy()
outlier_columns = [
'horizontal_displacement',
'vertical_displacement'
]
for col in outlier_columns:
if col in df.columns:
median = df[col].median()
mad = np.median(np.abs(df[col] - median))
# Modified Z-score 계산
modified_z_scores = 0.6745 * (df_clean[col] - median) / mad
# 임계값 이내의 데이터만 유지
mask = np.abs(modified_z_scores) <= mad_threshold
df_clean = df_clean[mask]
return df_clean
MAD vs 3-Sigma 비교:
| 방법 | 기준 | 장점 | 단점 |
|---|---|---|---|
| 3-Sigma | 평균, 표준편차 | 정규분포에서 효과적 | 아웃라이어의 영향 받음 |
| MAD | 중앙값 | 아웃라이어에 강건 | 정규분포 아닐 때 보수적 |
고정 로버처럼 아웃라이어가 많을 수 있는 경우 MAD 방법을 권장합니다.
5단계: 시계열 이동 중앙값 필터
점진적인 변화는 유지하면서 급격한 노이즈만 제거합니다.
def remove_outliers_rolling_median(df, window=20, threshold=3):
"""
이동 중앙값 기반 아웃라이어 제거
구조물의 점진적 변화는 보존
"""
df = df.sort_values('timestamp').reset_index(drop=True)
df_clean = df.copy()
outlier_columns = [
'horizontal_displacement',
'vertical_displacement'
]
for col in outlier_columns:
if col in df.columns:
# 이동 중앙값 계산
rolling_median = df[col].rolling(window=window, center=True).median()
# 중앙값으로부터의 편차
deviation = np.abs(df[col] - rolling_median)
rolling_mad = deviation.rolling(window=window, center=True).median()
# Modified Z-score
modified_z = 0.6745 * deviation / rolling_mad
# 임계값 이내만 유지
mask = modified_z <= threshold
mask = mask.fillna(True) # NaN은 유지
df_clean = df_clean[mask]
return df_clean
윈도우 크기 선택:
- 작은 윈도우(5-10): 빠른 변화 감지, 노이즈에 민감
- 큰 윈도우(20-50): 안정적, 느린 변화만 감지
구조물 모니터링에서는 20-30 정도의 큰 윈도우 권장
종합 파이프라인
위의 모든 단계를 통합한 완전한 파이프라인입니다.
def clean_fixed_rover_data(df, params=None):
"""
고정 로버 RTK GPS 데이터 정제 종합 파이프라인
"""
if params is None:
# 구조물 모니터링 권장 파라미터
params = {
'min_satellites': 12,
'max_hdop': 1.5,
'jump_threshold': 0.03, # 3cm
'mad_threshold': 3.5,
'rolling_window': 20
}
print(f"원본 데이터: {len(df)}개 점\n")
# 1단계: Fix 품질 필터링
df = filter_by_fix_quality(df)
print(f"1. Fix 품질 필터링: {len(df)}개 점")
# 2단계: 위성 품질 필터링
df = filter_by_satellite_quality(
df,
min_satellites=params['min_satellites'],
max_hdop=params['max_hdop']
)
print(f"2. 위성 품질 필터링: {len(df)}개 점")
# 3단계: 기준 위치 설정 및 변위 계산
baseline = calculate_baseline_position(df)
df = calculate_displacement(df, baseline)
print(f"3. 기준 위치 설정 완료")
print(f" Lat: {baseline['latitude']:.8f}")
print(f" Lon: {baseline['longitude']:.8f}")
print(f" Alt: {baseline['altitude']:.3f}m")
# 4단계: 급격한 점프 제거
df = remove_sudden_jumps(df, jump_threshold=params['jump_threshold'])
print(f"4. 급격한 점프 제거: {len(df)}개 점")
# 5단계: MAD 기반 아웃라이어 제거
df = remove_outliers_mad(df, mad_threshold=params['mad_threshold'])
print(f"5. MAD 필터링: {len(df)}개 점")
# 6단계: 시계열 이동 중앙값 필터
df = remove_outliers_rolling_median(
df,
window=params['rolling_window'],
threshold=3
)
print(f"6. 이동 중앙값 필터링: {len(df)}개 점")
print(f"\n최종 정제 데이터: {len(df)}개 점")
return df, baseline
# 사용 예시
df_clean, baseline = clean_fixed_rover_data(df_raw)
결과 분석 및 시각화
변위 통계 분석
def analyze_displacement_statistics(df):
"""
변위 통계 분석 및 리포트
"""
print("\n=== 변위 통계 분석 ===\n")
# 수평 변위 통계
print("수평 변위:")
print(f" 평균: {df['horizontal_displacement'].mean()*1000:.2f} mm")
print(f" 표준편차: {df['horizontal_displacement'].std()*1000:.2f} mm")
print(f" 최대: {df['horizontal_displacement'].max()*1000:.2f} mm")
print(f" 95% 신뢰구간: {df['horizontal_displacement'].quantile(0.95)*1000:.2f} mm")
# 수직 변위 통계
print(f"\n수직 변위:")
print(f" 평균: {df['vertical_displacement'].mean()*1000:.2f} mm")
print(f" 표준편차: {df['vertical_displacement'].std()*1000:.2f} mm")
print(f" 최대: {df['vertical_displacement'].max()*1000:.2f} mm")
print(f" 최소: {df['vertical_displacement'].min()*1000:.2f} mm")
# 총 변위량
total_displacement = df['vertical_displacement'].iloc[-1] - df['vertical_displacement'].iloc[0]
print(f" 총 침하/융기: {total_displacement*1000:.2f} mm")
# 정확도 평가 (2σ)
print(f"\n측정 정밀도 (2σ):")
print(f" 수평: {df['horizontal_displacement'].std()*2*1000:.2f} mm")
print(f" 수직: {df['vertical_displacement'].std()*2*1000:.2f} mm")
analyze_displacement_statistics(df_clean)
시각화
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter
def visualize_fixed_rover(df, baseline):
"""
고정 로버 데이터 종합 시각화
"""
fig = plt.figure(figsize=(16, 10))
# 1. 수평 변위 시계열
ax1 = plt.subplot(2, 3, 1)
ax1.plot(df['timestamp'], df['horizontal_displacement']*1000,
'b-', linewidth=0.5)
ax1.set_ylabel('수평 변위 (mm)')
ax1.set_title('수평 변위 시계열')
ax1.grid(True, alpha=0.3)
ax1.xaxis.set_major_formatter(DateFormatter('%H:%M'))
# 2. 수직 변위 시계열
ax2 = plt.subplot(2, 3, 2)
ax2.plot(df['timestamp'], df['vertical_displacement']*1000,
'r-', linewidth=0.5)
ax2.set_ylabel('수직 변위 (mm)')
ax2.set_title('수직 변위 시계열')
ax2.grid(True, alpha=0.3)
ax2.xaxis.set_major_formatter(DateFormatter('%H:%M'))
# 3. 수평면 궤적
ax3 = plt.subplot(2, 3, 3)
scatter = ax3.scatter(df['east_displacement']*1000,
df['north_displacement']*1000,
c=range(len(df)), cmap='viridis', s=1)
ax3.plot(0, 0, 'r*', markersize=15, label='기준점')
ax3.set_xlabel('동-서 변위 (mm)')
ax3.set_ylabel('남-북 변위 (mm)')
ax3.set_title('수평면 궤적')
ax3.axis('equal')
ax3.grid(True, alpha=0.3)
ax3.legend()
# 4. 변위 분포
ax4 = plt.subplot(2, 3, 4)
ax4.hist(df['horizontal_displacement']*1000, bins=50,
alpha=0.7, label='수평', edgecolor='black')
ax4.hist(df['vertical_displacement']*1000, bins=50,
alpha=0.7, label='수직', edgecolor='black')
ax4.set_xlabel('변위 (mm)')
ax4.set_ylabel('빈도')
ax4.set_title('변위 분포')
ax4.legend()
# 5. 위성 개수
ax5 = plt.subplot(2, 3, 5)
ax5.plot(df['timestamp'], df['num_satellites'], 'g-', linewidth=0.5)
ax5.set_ylabel('위성 개수')
ax5.set_title('위성 개수 변화')
ax5.grid(True, alpha=0.3)
ax5.xaxis.set_major_formatter(DateFormatter('%H:%M'))
# 6. HDOP
ax6 = plt.subplot(2, 3, 6)
ax6.plot(df['timestamp'], df['hdop'], 'orange', linewidth=0.5)
ax6.set_ylabel('HDOP')
ax6.set_title('HDOP 변화')
ax6.grid(True, alpha=0.3)
ax6.xaxis.set_major_formatter(DateFormatter('%H:%M'))
plt.tight_layout()
plt.show()
visualize_fixed_rover(df_clean, baseline)
실전 적용 가이드
파라미터 조정 가이드
용도에 따라 파라미터를 조정할 수 있습니다:
# 초정밀 구조물 모니터링 (댐, 교량 등)
params_precision = {
'min_satellites': 14,
'max_hdop': 1.2,
'jump_threshold': 0.02, # 2cm
'mad_threshold': 3.0, # 더 엄격
'rolling_window': 30
}
# 일반 구조물 모니터링
params_standard = {
'min_satellites': 12,
'max_hdop': 1.5,
'jump_threshold': 0.03, # 3cm
'mad_threshold': 3.5,
'rolling_window': 20
}
# 긴급 상황 (데이터 부족 시)
params_relaxed = {
'min_satellites': 10,
'max_hdop': 2.0,
'jump_threshold': 0.05, # 5cm
'mad_threshold': 4.0, # 더 관대
'rolling_window': 15
}
데이터 수집 권장사항
1. 샘플링 주파수
- 1Hz (1초마다): 표준, 대부분의 경우 충분
- 5Hz 이상: 동적 구조물, 더 정밀한 분석 필요 시
2. 관측 기간
- 최소 24시간: 일일 변화 패턴 파악
- 7일 이상: 주간 패턴, 환경 영향 분석
- 장기 모니터링: 수개월~수년
3. 환경 조건
- 안테나 위치: 하늘이 최대한 열린 곳
- 주변 장애물: 건물, 나무 등으로부터 충분한 거리
- 전원 안정성: UPS 등으로 연속 측정 보장
경보 시스템 구축
실시간 모니터링을 위한 경보 시스템:
def check_displacement_alarm(df, thresholds):
"""
변위 임계값 초과 시 경보
"""
# 최근 10개 데이터의 평균으로 판단 (순간적 노이즈 방지)
recent_data = df.iloc[-10:]
current_horizontal = recent_data['horizontal_displacement'].mean()
current_vertical = recent_data['vertical_displacement'].mean()
alerts = []
if abs(current_horizontal) > thresholds['horizontal']:
alert_msg = f"⚠️ 수평 변위 경고: {current_horizontal*1000:.1f}mm"
alerts.append(alert_msg)
print(alert_msg)
if current_vertical < -thresholds['vertical_subsidence']:
alert_msg = f"⚠️ 침하 경고: {current_vertical*1000:.1f}mm"
alerts.append(alert_msg)
print(alert_msg)
if current_vertical > thresholds['vertical_uplift']:
alert_msg = f"⚠️ 융기 경고: {current_vertical*1000:.1f}mm"
alerts.append(alert_msg)
print(alert_msg)
return alerts
# 임계값 설정 (구조물 종류에 따라 조정)
thresholds = {
'horizontal': 0.05, # 수평 5cm
'vertical_subsidence': 0.10, # 침하 10cm
'vertical_uplift': 0.05 # 융기 5cm
}
alerts = check_displacement_alarm(df_clean, thresholds)
고급 기법: Kalman 필터
더 정밀한 분석이 필요한 경우, Kalman 필터를 추가로 적용할 수 있습니다.
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
def apply_kalman_filter(df):
"""
Kalman 필터로 노이즈 제거 및 아웃라이어 감지
"""
df = df.sort_values('timestamp').reset_index(drop=True)
# 3차원 위치에 대한 Kalman 필터
kf = KalmanFilter(dim_x=3, dim_z=3)
# 초기 상태
kf.x = np.array([
df['east_displacement'].iloc[0],
df['north_displacement'].iloc[0],
df['vertical_displacement'].iloc[0]
])
# 상태 전이 행렬 (위치만, 속도 없음)
kf.F = np.eye(3)
# 관측 행렬
kf.H = np.eye(3)
# 프로세스 노이즈 (구조물은 천천히 변함)
kf.Q = Q_discrete_white_noise(dim=3, dt=1.0, var=0.0001)
# 측정 노이즈 (RTK GPS 정확도: ~1cm)
kf.R = np.eye(3) * 0.01**2
# 필터링 실행
filtered_positions = []
innovations = []
for idx, row in df.iterrows():
kf.predict()
z = np.array([
row['east_displacement'],
row['north_displacement'],
row['vertical_displacement']
])
kf.update(z)
# Innovation (측정값 - 예측값)
innovation = z - kf.x
innovations.append(np.linalg.norm(innovation))
filtered_positions.append(kf.x.copy())
# Innovation이 큰 점을 아웃라이어로 판정
innovations = np.array(innovations)
threshold = np.median(innovations) + 3 * np.std(innovations)
outlier_mask = innovations > threshold
df_clean = df[~outlier_mask].copy()
# 필터링된 위치 저장
filtered_positions = np.array(filtered_positions)
df_clean['filtered_east'] = filtered_positions[~outlier_mask, 0]
df_clean['filtered_north'] = filtered_positions[~outlier_mask, 1]
df_clean['filtered_vertical'] = filtered_positions[~outlier_mask, 2]
return df_clean
# Kalman 필터를 파이프라인에 추가
df_kalman = apply_kalman_filter(df_clean)
Kalman 필터의 장점:
- 측정 노이즈와 실제 변위를 통계적으로 분리
- 점진적 변화를 더욱 부드럽게 추정
- 예측 기능으로 다음 측정값 예상 가능
주의사항:
- 파라미터 튜닝이 중요 (Q, R 행렬)
- 계산량이 많아 실시간 처리 시 고려 필요
방법론 비교 및 선택 가이드
각 방법의 특성
| 방법 | 강점 | 약점 | 적용 시점 |
|---|---|---|---|
| Fix/위성 필터 | 명확한 기준, 빠름 | 품질 좋은 데이터도 손실 가능 | 1차 필터링 |
| 급격한 점프 제거 | 명백한 오류 제거 | 실제 급격한 변화 시 문제 | 2차 필터링 |
| MAD | 아웃라이어에 강건 | 정규분포 아닐 때 보수적 | 핵심 방법 |
| 이동 중앙값 | 점진적 변화 보존 | 윈도우 크기 선택 중요 | 시계열 특화 |
| Kalman 필터 | 정밀도 최고 | 복잡, 파라미터 조정 필요 | 고급 분석 |
권장 조합
기본 조합 (대부분의 경우):
- Fix/위성 필터
- 급격한 점프 제거
- MAD 필터
정밀 조합 (고정밀도 요구 시):
- Fix/위성 필터 (엄격)
- 급격한 점프 제거
- MAD 필터
- 이동 중앙값 필터
- Kalman 필터
빠른 조합 (실시간 처리):
- Fix/위성 필터
- 급격한 점프 제거
실제 적용 사례
Case 1: 교량 모니터링
상황: 대형 교량의 처짐 측정
요구사항: mm 단위 정밀도
적용 방법:
- 1Hz 샘플링, 24시간 연속 측정
- 엄격한 Fix 필터 (Fixed RTK only)
- MAD 필터 + 이동 중앙값
- Kalman 필터 추가
결과:
- 수직 정밀도: ±2mm (2σ)
- 일일 온도 변화에 따른 3-5mm 처짐 감지 성공
Case 2: 댐 안전 모니터링
상황: 댐 제체의 수평/수직 변위 장기 모니터링
요구사항: 장기 추세 분석
적용 방법:
- 1Hz 샘플링, 연속 측정
- 표준 파라미터 세트
- 주간 단위 데이터 검토
결과:
- 연간 2mm 침하 추세 확인
- 강우 시 일시적 변위 패턴 발견
Case 3: 지반 침하 모니터링
상황: 도심지 터널 공사 주변 지반 침하
요구사항: 실시간 경보
적용 방법:
- 5Hz 샘플링
- 빠른 조합 (실시간 처리)
- 자동 경보 시스템 연동
결과:
- 일일 1mm 침하 감지 및 경보
- 공사 안전 관리 강화
결론
RTK GPS를 이용한 구조물 모니터링에서 정확한 변위 측정을 위해서는 체계적인 아웃라이어 검출이 필수적입니다. 본 글에서 소개한 방법들은 다음과 같은 순서로 적용하는 것을 권장합니다:
- 품질 기반 1차 필터링: Fix 상태, 위성 개수, HDOP
- 기준 위치 설정: 중앙값 기반 안정적 기준점
- 급격한 변화 제거: 물리적으로 불가능한 점프 제거
- 통계적 필터링: MAD 또는 3-Sigma
- 시계열 필터링: 이동 중앙값으로 점진적 변화 보존
- 고급 필터링 (선택): Kalman 필터로 최종 정밀도 향상
각 구조물의 특성과 요구사항에 맞춰 파라미터를 조정하고, 지속적인 모니터링과 검증을 통해 최적의 설정을 찾는 것이 중요합니다.